Motivation

Suppose you are only one in the world who is in the possession of the following polynomial \(f(x)\) of the form:

\[ f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_d x^d, \tag{1} \]

where \(d\) is the degree of the polynomial.

What will you do if your friend wants the evaluation of this polynomial \(f(x)\) at some point \(x = 10\)?

The first option would be that you can just share your polynomial with your friend and then your friend can evaluate the polynomial \(f(x)\) for himself. But what if the polynomial is very "big", that is, have very large degree \(d\) and your friend has very limited compute resource? Even with optimal methods like Horner's method, eveluating the polynomial \(f(x)\) would take \(d\) multiplication and \(d\) addition operations. Additionally, it could also be the case that the message channel between you and your friend has limited capacity. You might wonder that with computers being so powerful and network bandwidth being so high, how is it possible to be resource-constrained. To give you a practical example, let us consider your friend to be Ethereum post-EIP 4844 (proto-danksharding). Here, the degree \(d\) of the polynomial can go upto \(4096\) and each evaluation point will be of size 32 bytes (let us ignore what this "big" polynomial is going to be used for). Now, unless you want to pay for high gas, your friend Ethereum's compute and bandwidth resource is all resource-constrained.

The alternative option would be for you to do the evaluation of the polynomial \(f(x)\) at the point \(x = 10\) and send it to your friend. However, there is a catch as shown in the following conversation:

The catch is in how can your friend verify that the value \(y\) you sent is equal to \(f(10)\). One way to accomplish that would be to send the whole polynomial \(f(x)\), that is its coeficients \(a_i \hspace{0.1cm} \forall i \in \{0, \cdots, d\}\), which your friend can use to evaluate \(f(10)\) and check that \(y == f(10)\) or not. But then we encounter the aforementioned resource-constraints. Additionally, it could be the case that out of privacy concerns, you don't want to reveal your polynomial \(f(x)\) to anyone, even to your friend.

Intuition

Referring to Fig.1, a wishful thinking would be what if you can generate a "very short" evidence \(\pi\) such that:

• you can send the evidence \(\pi\) to your friend along with the value \(y\) that would convince your friend \(y == f(10)\), and
• this evidence \(\pi\) doesn't reveal anything to your friend about your polynomial \(f(x)\). This property is called hiding.

If we have such an evidence, it seems we are all set.

But wait! Let us reverse the scenario - now your friend is claiming to be in posession of the polynomial \(f(x)\) and you want evaluation of \(f(x)\) at point \(x=10\). Would you be willing to trust your friend that she gave you the evaluation of the same polynomial for which she claimed to be in possession of?

One very natural way to solve this trust issue is to have your friend first send a short representation \(C\) of the polynomial \(f(x)\) she is in possession of. Sending this short representation is like a "commitment" that your friend is making to you about the polynomial \(f(x)\) she is in possession of. This property is called as polynomial binding. Now, later when you send your evaluation point, your friend would send the evidence \(\pi\) of correct evaluation which you can use along with the commitment \(C\) to verify that your friend did everything correctly!

The following conversation illustrates the above intuition.

This above intuition is formalized in the KZG polynomial commitment protocol as described in the next section.

It is very important that your friend sends you the commitment \(C\) before you send your evaluation point. Otherwise, your friend can fool you by sending a correct evaluation for a polynomial that is different from the polynomial \(f(x)\) she was claiming to be in possession of.

KZG Protocol

KZG polynomial commitment was proposed by Kate (pronounced as "Katey"), Zaverucha and Goldberg in this paper back in 2010. In a change of notation that we will be following consistently from now on, we will call the person claiming to be in possession of polynomial \(f(x)\) as "prover" and the other person who wants an evaluation of that polynomial \(f(x)\) (recall that this person doesn't know the coeffcients of \(f(x)\)) as "verifier".

In order to construct the protocol around the intuition present in previous section, we will take help of cyclic groups and bilinear pairing that have been described in this note. The protocol proceeds in multiple steps and the pattern that you see here is followed in the more complex protocols that you will read later.

1. Setup

Okay, this might sound very weird at first but the first step of KZG protocol is to have a ceremony where many folks (preferrably hundreds and thousands of people from around the world) come together to contribute towards constructing a special object called powers-of-tau. I am sure this might not be apparent but powers-of-tau and its security is super-critical to get the property of polynomial binding and hiding. This will be made clear later, please bear patience with me 🤗.

Construction of powers-of-tau requires everyone to first come to an agreement on the following core parameter assumptions:

• three groups \(G_1\), \(G_2\) and \(G_T\),
• a bilinear mapping called pairing \(e: G_1 \times G_2 \rightarrow G_T\) over these three groups,
• two positive integers \(d_1\) and \(d_2\).

You can see this spec for ETH2 PoS to get an idea how these parameters look like.

Once this done, the power-of-tau ceremony is initiated where each participant has to choose their own random secret and then add it to a running aggregate of all random secrets added before by others. Note that you will not be able to know the random secrets of other people just by looking at the running aggregate. You can read more about how this ceremony achieves this property here . At a high-level this important property is inherited from DL hardness assumption (see here) and is necessary for KZG protocol to be secure.

At the end of the ceremony, the powers-of-tau setup looks something like this: $$ \begin{align} &\{[1]_1, [s]_1, [s^2]_1, \cdots, [s^{d_1}]_1 \}, \\ &\{[1]_2, [s]_2, [s^2]_2, \cdots, [s^{d_2}]_2 \} \end{align} $$ Please check this for further details on the above notations. Now,

One question is how large the size this powers-of-tau setup should be. Basically, how big is \(d_1\) and \(d_2\). That is completely dependent upon the system designer on how big of a polynomial do they want to support.

Once the powers-of-tau ceremony is over, it is critical that at least one of the participants is honest and destroys the random secret it contributed. This ensures that the aggregate secret \(s\) remains random to everyone, even if they look at the powers-of-tau 🤙.

2. Commit

This step is for the prover to bind itself to the polynomial \(f(x)\) that it is in possession of, aka polynomial binding. In order to do so, the prover's just have to evaluate the commitment \(C\) given by \[ C = [f(s)]_1 \tag{2}\] where \(s\) is the secret obtained during powers-of-tau ceremony that no one is supposed to know. You might be wondering that if secret \(s\) is unknown, then how the hell the prover is going to evaluate the commitment \(C\).

The trick here is to do linear combination of the group elements on the powers-of-tau. Recalling eq.(1), we have: $$ \begin{align} [f(s)]_1 &= [a_0 + a_1 s + a_2 s^2 + \cdots + a_d s^d]_1, \quad \quad \text{from eq. (1)}\\ &= (a_0 + a_1 s + a_2 s^2 + \cdots + a_d s^d) \cdot g_1 \\ &= a_0 \cdot g_1 + (a_1 s) \cdot g_1 + (a_2 s^2) \cdot g_1 + \cdots + (a_d s^d) \cdot g_1 \\ &= a_0 \cdot g_1 + a_1 \cdot (s \cdot g_1) + a_2 \cdot (s^2 \cdot g_1) + \cdots + a_d \cdot (s^d \cdot g_1) \\ &= a_0 \cdot [1]_1 + a_1 \cdot [s]_1 + a_2 \cdot [s^2]_1 + \cdots + a_d \cdot [s^d]_1. \end{align} $$ With this re-writing, the prover can compute the commitment \(C\) by picking the first \(d\) elements from the first vector in powers-of-tau, do a scalar multiplication on each of these points on the group \(G_1\) using their respective coefficients in \(f(x)\) and then add them. This process is commonly referred to as Multi-Scalar Multiplication (MSM). One important thing to observe that in order for above computation to be even possible, it is necessary that \(d \leq d_1 \). Finally,

3. Challenge

In this step, the verifier needs to inform the prover that at what point \(\alpha \in \mathcal{F}\) does it want the evaluation of \(f(x)\) at.

4. Create witness

Given that the verifier wants the polynomial \(f(x)\) to be evaluated at \(x=\alpha\), the prover now also has to compute a proof \(\pi\) that can convince the verifier that prover did the evaluation correctly. To understand how this proof is constructed, we go back to polynomial division that we all learnt in schools 🤓.

Suppose we take a constant polynomial \(g(x)\) as defined by: $$ g(x) = f(\alpha) \quad \forall x = \alpha.$$ If we subtract this polynomial \(g(x)\) from \(f(x)\) as shown in the following animation, we end up getting the polynomial \(f(x) - g(x)\) which equals to \(0\) at \(x=\alpha\). What this means is that \(x=\alpha\) is a root of the polynomial \(f(x) - g(x)\).

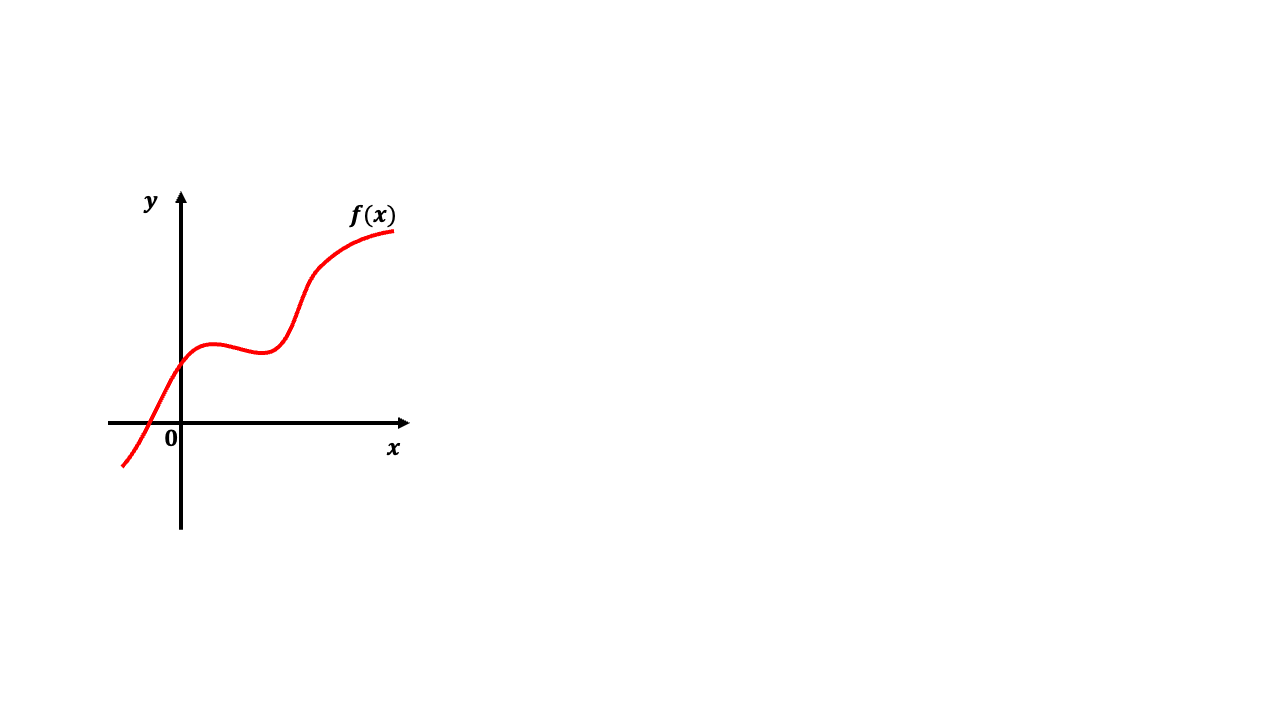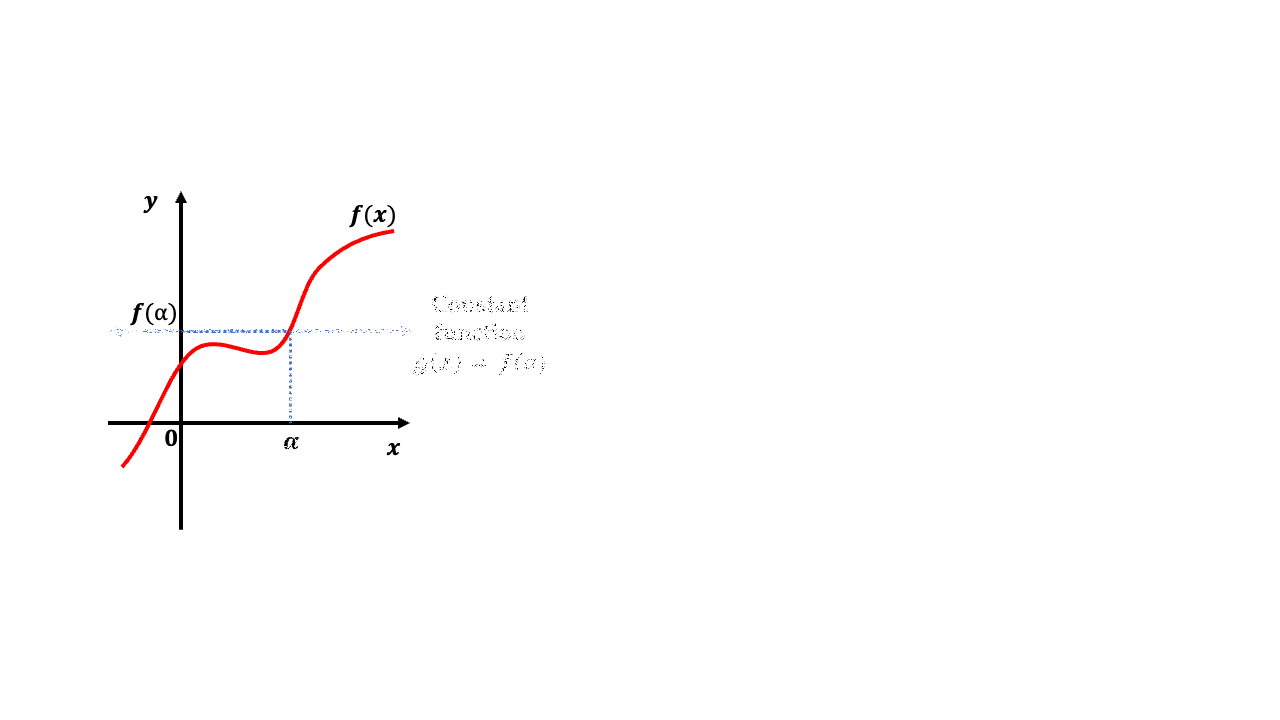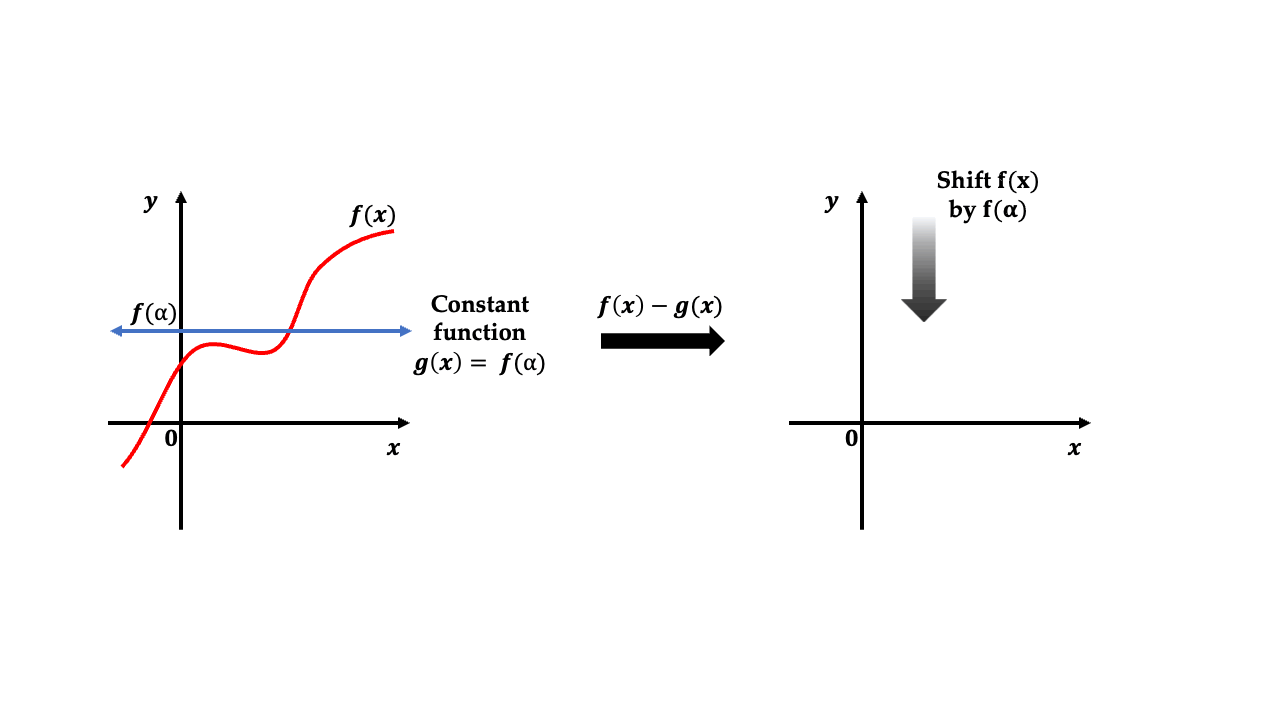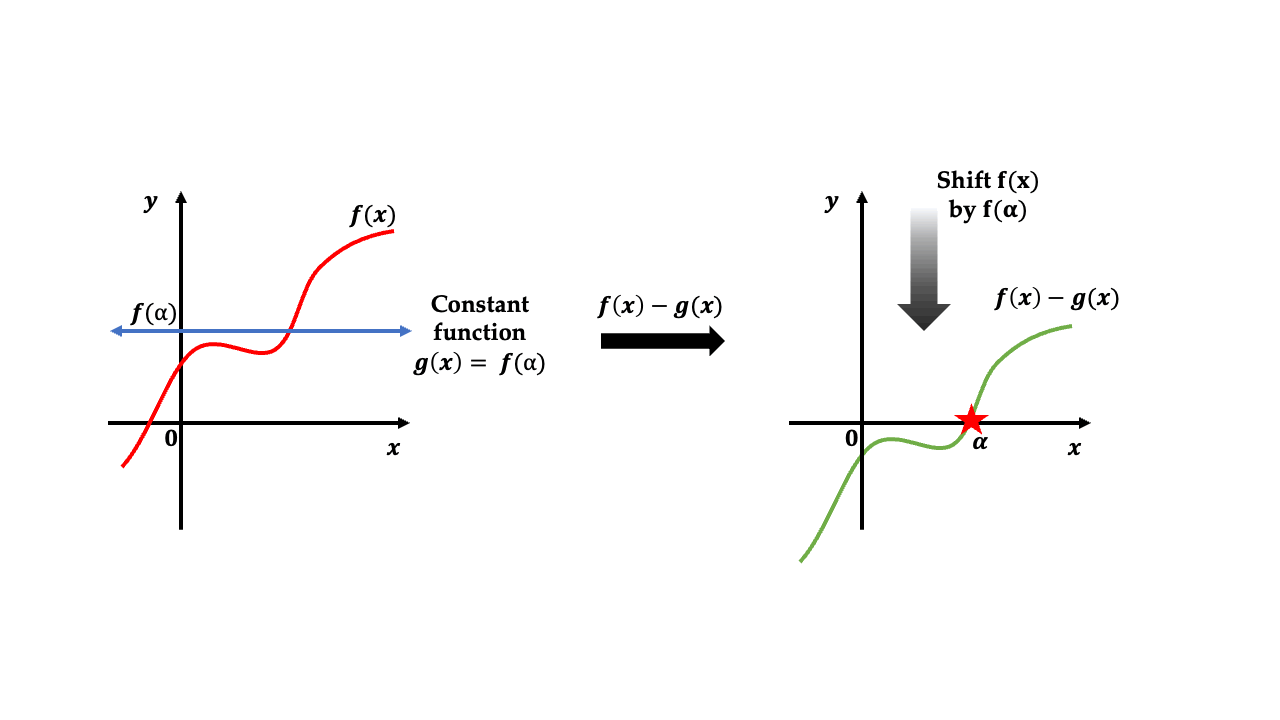
A very nice property of polynomials is that \(x=\alpha\) is root of a given polynomial if and only if this polynomial is divisible by \((x-\alpha)\) 😮. Therefore, our polynomial \(f(x) - g(x)\) is also divisible by \(x-\alpha\). This can be written down as: $$ f(x) - g(x) = f(x) - f(\alpha) = (x-\alpha) Q(x) \tag{3}$$ for some polynomial \(Q(x)\) whose degree is less than that of \(f(x) - f(\alpha)\). In the second equality, we used the fact that \(g(x)\) is constant polynomial. For the prover, we now have:

Solving this translated problem is much easier using pairings. As part of that process, the prover uses the polynomial \(Q(x)\) obtained before to generate the proof \(\pi\): $$ \pi = [Q(s)]_1 \tag{4}$$ where \(s\) is the secret obtained from powers-of-tau ceremony. We use the same linear combination of elements from powers-of-tau as in step 2 to generate \(\pi\). Finally,

5. Verify evaluation

Observe that the verifer now has the following data in its possession:

• point \(\alpha\)
• commitment \(C\) from the verifier,
• proof \(\pi\) from the verifier,
• evaluation \(y\) from the verifier.

All now the verifier has to check is whether these four data points satisfy eq. (3) or not. However, now the issue is \(\alpha, y \in \mathbb{F}\) and \(C, \pi \in G_1\). This is where we will be using the awesome capabilities of pairings 😎. The verifer simply checks that $$ e(\pi, [s - \alpha]_2) \stackrel{?}{=} e(C - [y]_1, [1]_2). \tag{5}$$ To understand the intuition why this verification works, let us consider the scenario where the prover is honest. Unwrapping the LHS of eq. (5), we have $$ \begin{align} e(\pi, [s - \alpha]_2) &= e( [Q(s)]_1, [s - \alpha]_2) \\ &= e\Bigg( \Big[\frac{f(s) - f(a)}{s-a}\Big]_1, [s - \alpha]_2\Bigg) \text{ where we used eq. (3) and (4)}\\ &= e([1]_1, [s - \alpha]_2)^{\frac{f(s) - f(a)}{s-a}} \\ &= e([1]_1, [1]_2)^{\left[\frac{f(s) - f(a)}{s-a}\right] (s - \alpha)} \\ &= e([1]_1, [1]_2)^{f(s) - f(a)} \\ &= e([f(s) - f(a)]_1, [1]_2) \\ &= e((f(s) - f(a))\cdot g_1, [1]_2) \\ &= e(f(s) \cdot g_1 - f(a) \cdot g_1, [1]_2) \\ &= e(C - [f(a)]_1, [1]_2) \text{ where we used eq. (2)} \end{align} $$

5.1. KZG protocol in production on Ethereum

Observe that \([s - \alpha]_2 = (s - \alpha)\cdot g_2 = s \cdot g_2 - \alpha \cdot g_2 = [s]_2 - [\alpha]_2 = [s]_2 - \alpha \cdot [1]_2\). The verifier can compute \( \alpha \cdot [1]_2\) by scalar multiplication of \(\alpha\) with \([1]_2\) (which is the first element of second vector in the power-of-tau setup) on \(G_2\). However, most of you will be running verifier as a smart contract on Ethereum. Unfortunately, EVM provides for precompiled code by the name ec-Mul for doing scalar multiplication only on \(G_1\) 😓.

The trick that you must use in production involves re-writing eq. (5) as: $$ \begin{align} & e(\pi, [s - \alpha]_2) \stackrel{?}{=} e(C - [y]_1, [1]_2)\\ \implies & e(\pi, (s - \alpha)\cdot g_2) \stackrel{?}{=} e(C - [y]_1, [1]_2) \\ \implies & e(\pi, s\cdot g_2 - \alpha \cdot g_2) \stackrel{?}{=} e(C - [y]_1, [1]_2) \\ \implies & e(\pi, s\cdot g_2) e(\pi, - \alpha \cdot g_2) \stackrel{?}{=} e(C - [y]_1, [1]_2) \\ \implies & e(\pi, s\cdot g_2) e(\pi, \alpha \cdot g_2)^{-1} \stackrel{?}{=} e(C - [y]_1, [1]_2) \\ \implies & e(\pi, s\cdot g_2) \stackrel{?}{=} e(C - [y]_1, [1]_2) e(\pi, \alpha \cdot g_2) \\ \implies & e(\pi, [s]_2) \stackrel{?}{=} e(C - [y]_1, [1]_2) e(\pi, [1]_2)^{\alpha} \\ \implies & e(\pi, [s]_2) \stackrel{?}{=} e(C - [y]_1, [1]_2) e(\alpha \cdot \pi, [1]_2)\\ \implies & e(\pi, [s]_2) \stackrel{?}{=} e(C - [y]_1 + \alpha \cdot \pi, [1]_2) \end{align} $$

With the above equivalent verification check in hand, the verifier would instead first compute \([y]_1\) by scalar multiplication of \(y\) with \([1]_1\) (obtained from powers-of-tau setup) using ec-Mul precompiled op-code 😌. A similar scalar multiplication is done between the scalar \(\alpha\) and the proof \(\pi\). Now, point addition on \(G_1\) is done among \(C, [y]_1\) and \(\alpha \cdot \pi\). For your convenience, EVM provides precompiled code by the name ec-Add that you can use to do point addition on G_1 😌.

Why does the KZG protocol work?

Y'all might be curious why does this alien-looking equation works? Well,